Vienna
06-8) 힙 정렬 본문
오늘치 백준 문제를 풀려고 보니 힙정렬에 대한 언급이 나와 힙정렬에 대해 먼저 공부하고 싶었다.
◇ 힙?
부모의 값이 자식의 값보다 항상 크다는 조건을 만족하는 완전이진트리.
(이때 부모의 값이 자식보다 항상 작아도 힙이라고 한다. 부모와 자식 요소의 관계만 일정하면 된다.)
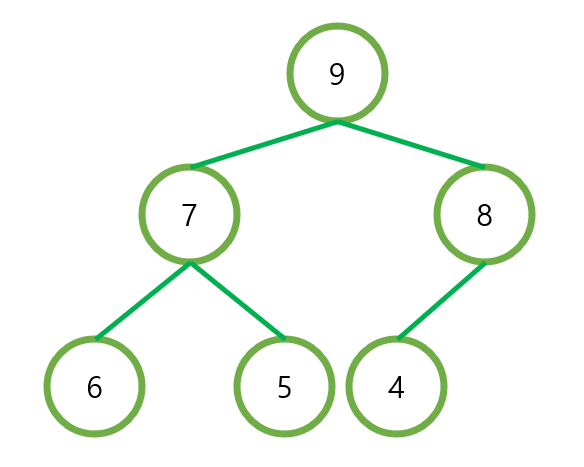
- 부모와 자식 관계는 일정.
- 형제 사이의 대소 관계는 일정하지 않다.
- 이 때문에 부분순서트리(parttial ordered tree)라고도 한다.
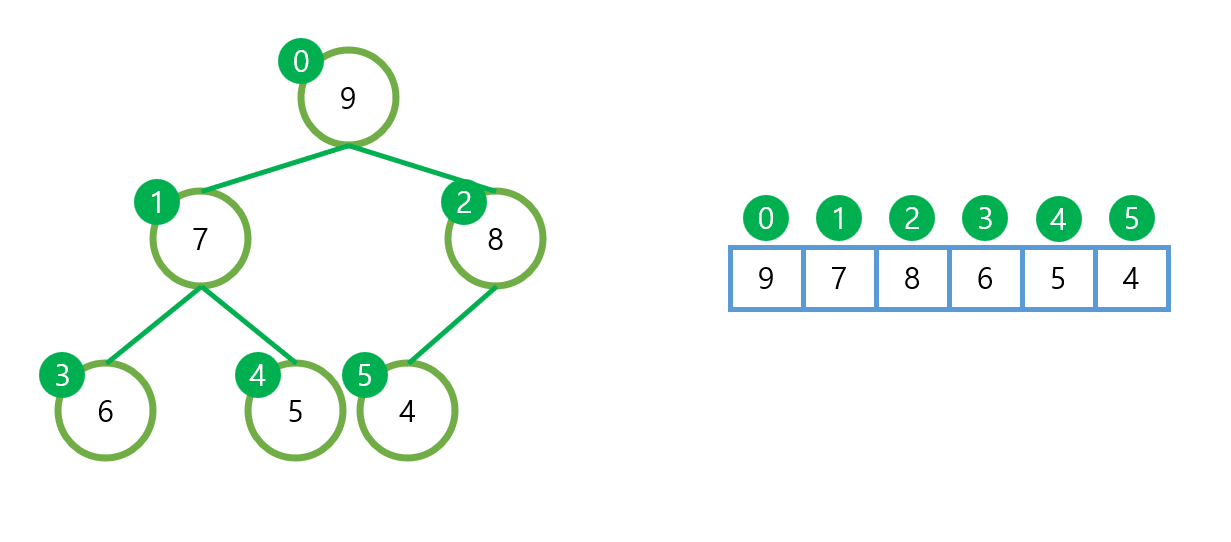
힙의 요소를 배열에 저장하면 부모와 자식의 인덱스 사이에 다음과 같은 관계 성립
- 부모는 a[(i-1)/2]
- 왼쪽 자식은 a[(i-1)/2+1]
- 오른쪽 자식은 a[(i-1)/2+2]
◇ 힙 정렬?
선택 정렬을 응용한 알고리즘. 힙(heap)의 특성을 이용하여 정렬을 수행한다.
즉, "가장 큰 값이 루트에 위치"한다는 특징을 이용하는 정렬 알고리즘.
힙에서 가장 큰 값인 루트를 꺼내는 작업을 반복하고 그 값을 늘어놓으면 배열이 정렬을 마치게 되는 것.
아랫부분의 작은 부분트리부터 시작해 올라가는 방식(bottom-up)으로 전체 배열을 힙으로 만들 수도 있다.
◇ 루트 제거하고 힙 상태유지하기
- 루트를 꺼낸다.
- 마지막 요소를 루트로 이동한다.
- 자기보다 큰 값을 가지는 자식 요소와 자리를 바꾸며 아래로 내려가는 작업 반복.
- 단, 자식의 값이 작거나 잎에 다다르면 작업이 종료.
◇ 힙 정렬 알고리즘 단계
- 힙의 루트 a[0]에 있는 가장 큰 값을 꺼내 배열의 마지막 요소 a[a.length-1]와 바꾼다.
- 가장 큰 값을 a[a.length-1]로 옮기게 되면 a[a.length-1]는 정렬을 마치게 된다.
- a[0]~a[a.length-2]의 요소를 힙 상태로 만든다.
- 그 결과 두 번쨰로 큰 요소인 값이 루트에 위치하게 된다.
- 힙 루트에 있는 두 번째로 큰 값인 a[0]을 꺼내 a[a.length-2]와 바꾼다.
- 계속 반복한다.
#include <stdio.h>
#include <stdlib.h>
#define swap(type, x, y) do { type t = x; x = y; y = t;} while(0)
/// <summary>
/// 힙 상태로 만들어 준다.
/// </summary>
static void downheap(int a[], int left, int right) {
// 루트 (가장 큰 값)
int temp = a[left];
int child, parent;
for (parent = left; parent < (right + 1) / 2; parent = child) {
int cl = parent * 2 + 1;
int cr = cl + 1;
child = (cr <= right && a[cr] > a[cl]) ? cr : cl;
if(temp >=a[child])
break;
a[parent] = a[child];
}
a[parent] = temp;
}
void heapsort(int a[], int n) {
int i;
for (i = (n - 1) / 2; i >= 0; i--) {
// 힙상태가 아닐 수 있는 배열을 힙 상태로 먼저 만들어 준다.
downheap(a, i, n - 1);
}
for (i = n - 1; i > 0; i--) {
// 루트값과 현재 정렬되지 않은 마지막 index에 위치한 값을 바꿔준다.
swap(int, a[0], a[i]);
// 힙 상태로 만들어준다.
downheap(a, 0, i-1);
}
}
int main()
{
int i, nx;
int* x;
puts("힙 정렬");
printf("요소 개수: ");
scanf("%d", &nx);
x = (int*)calloc(nx, sizeof(int));
for (i = 0; i < nx; i++) {
printf("x[%d]", i);
scanf("%d", &x[i]);
}
heapsort(x, nx);
puts("오름차순으로 정렬했습니다");
for (i = 0; i < nx; i++) {
printf("x[%d] = %d", i, x[i]);
}
free(x);
return 0;
}너무 오랜만에 C언어로 알고리즘 문제를 푸는 거라 좀 어색하다;;
일단 풀어보자.
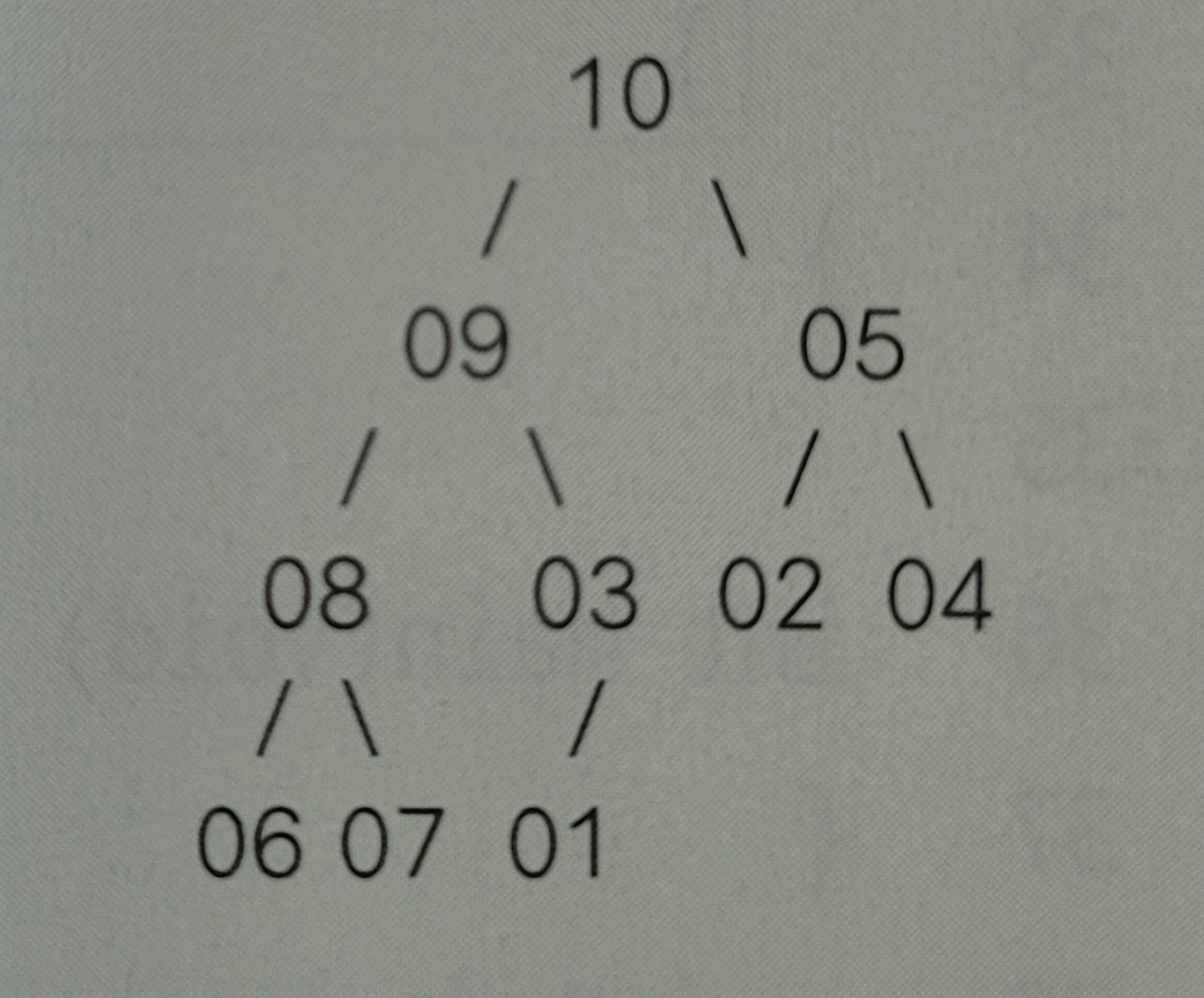
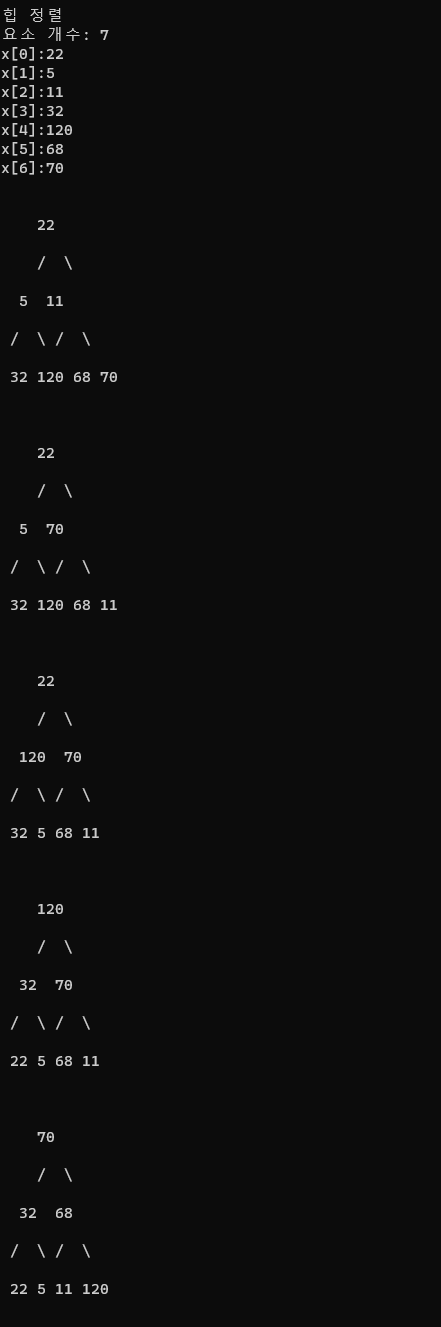
◇ Q22: downheap 함수가 호출될 때마다 오른쪽 그림처럼 배열의 값을 트리 형식으로 출력하는 프로그램을 작성하세요.
우선 가운데 정렬을 하기 위해서는 몇 층의 트리가 만들어질 것인지 예측이 가능해야 한다. 몇 층의 트리가 나올지는 어떻게 계산할 수 있을까?
오른쪽의 그림을 보면 0층은 1개, 1층은 2개, 2층은 4개, 3층은 8개, ... 즉, 2의 거듭제곱 형식으로 증가하는 추세임을 볼 수 있다.
그럼 구하고자하는 요소의 개수가 X개일 때, 층은 다음과 부등식의 최대 값이라고 볼 수 있다.
$$X \leq \sum_{n=0}^{n} 2^n $$
즉, 층을 구하는 코드는 다음과 같이 표현할 수 있다.
int calculateFloor(int n) {
const int correction = 2;
int result = 0;
int sum;
for (int j = 1, sum = j; sum < n; j *= correction, sum += j) {
result++;
}
return result;
}전체 층 tf를 구한 뒤에는 어떻게 하면될까?
현재 표현하려는 층 cf =0이고 1씩 증가한다면 왼쪽에 공간을 (tf - cf-1) * 3만큼 주면 될 것처럼 보인다.
$$space = (tf-cf-1)*3$$
inline int calculateSpace(int tf, int cf) {
const int correction = 3;
return (tf - cf - 1) * correction;
}문자(/ 와 \)를 출력해야하는 층은 어떻게 계산하면 좋을까? 이전 공백 사이즈의 -1을 하면 되지 않을까 싶다
자 그럼 한 번 문제를 풀어보면 다음과 같다.
완전히 예쁜 모양은 아니지만 완성이다.
int calculateFloor(int n) {
const int correction = 2;
int result = 0;
int sum;
for (int j = 1, sum = j; sum < n; j *= correction, sum += j) {
result++;
}
return result + 1;
}
inline int calculateSpace(int tf, int cf) {
const int correction = 3;
return (tf - cf - 1) * correction;
}
void printTree(int a[], int n) {
puts("\n");
const int correction = 2;
int tf, i, j, sum;
tf = calculateFloor(n);
for (int cf = 0, i = 0, j = 1, sum = 0; cf < tf; cf++, j *= correction) {
// 현재 층의 공백을 계산한다.
int space = calculateSpace(tf, cf);
int start = sum;
sum += j;
int end = sum;
for (int k = start; k < end && k < n; k++) {
for (int s = 0; s <= space / correction; s++) {
printf(" ");
}
printf("%d", a[k]);
}
puts("\n");
if (cf + 1 < tf) {
for (int k = start; k < end && k < n; k++) {
for (int s = 0; s < space - 2; s++) {
printf(" ");
}
printf("/ \\");
}
puts("\n");
}
}
}
일전에 배운대로 %*s를 쓰고 싶었는데 잘 적용되지 않아 for문을 돌면서 공백을 넣는 형태로 바꾸었다.
나중에 기회되면 적용해보고 싶다.
'알고리즘 문제 풀이 > Do It! 자료구조와 함께 배우는 알고리즘 입문 C언어 편' 카테고리의 다른 글
| 7일차 (0) | 2021.11.26 |
|---|---|
| 6일차 (0) | 2021.11.25 |
| 5일차 (5) (0) | 2021.11.24 |
| 5일차 (4) (0) | 2021.11.23 |
| 5일차 (3) (0) | 2021.11.23 |


