Vienna
백준26008번) 해시 해킹 본문
https://www.acmicpc.net/problem/26008
26008번: 해시 해킹
첫째 줄에 비밀번호의 길이 $N$과 문자 종류의 개수 $M$, 정수 $A$가 주어진다. ($1 \le N, M, A \le 5\,000\,000$) 둘째 줄에 재현이가 알아낸 해시값 정수 $H$가 주어진다. ($0 \le H < M$)
www.acmicpc.net
◇ 문제
그린닷컴의 운영자 연두는 비밀번호를 평문 그대로 저장하는 과오를 뒤로하고, 이제부터 암호에 해시 함수를 적용해 저장하려고 한다. 연두가 아는 해시 함수라고는 알고리즘 문제 풀이에 많이 사용되는 롤링 해시 함수밖에 없기 때문에 이것을 응용하여 사용하기로 했다.
그린닷컴의 비밀번호 규칙은 꽤 특이한데, 길이가 정확히 N이어야 하며, 비밀번호를 이루는 문자는 지정된 M의 문자 중 하나여야 한다.
따라서, 사용 가능한 각 문자를 0부터 차례대로 정수에 대응시키면, 비밀번호를 길이가 N이고 모든 원소가 0 이상 M-1이하인 배열을 아래와 같이 나타낼 수 있다.
$$P = [P_0, P_2, P_3, ... , P_{N-1}]$$
이렇게 비밀번호를 배열 P나타낸 후, 미리 정해진 정수 A를 이용하여 다음과 같은 해시 함수 h를 적용한다.

그린닷컴 관리자 계정의 비밀번호 해시값을 해킹한 재현이는, 이 해시값으로 실제 비밀번호가 뭐였는지 역추적해보려고 한다. 하지만 그린닷컴에서 사용 가능한 비밀번호는 M^N개나 있고, 이 중 과연 알아낸 해시값과 일치하는 비밀번호는 몇 개나 될지 궁금해졌다. 여러분이 이것을 대신 구해주자.
◇ 입력
첫째 줄에 비밀번호의 길이 N과 문자 종류의 개수 M, 정수 A가 주어진다. (1<=N, M, A <= 5,000,000)
둘째 줄에 재현이가 알아낸 해시값 정수 H가 주어진다. (0<=H<M)
◇ 출력
주어진 해시값을 갖는 비밀번호의 개수를 출력한다. 출력하는 값이 너무 커질 수 있으므로, 이것을 1 000 000 007 (10^9+7)로 나눈 나머지를 출력한다.
◆ 풀이
최근에 배운 수열의 개념을 활용할 문제가 나왔다.
우선 h(P)를 수식으로 표현하면 아래와 같다.
$$h(P) = \sum_{n=0}^{N-1} P_{n}\cdot A^{n} \bmod M$$
그리고 이 식은 다음과 같이 표현할 수 있다.
$$h(P) = (P_0\cdot A^0 + \sum_{n=1}^{N-1} P_n\cdot A^n) \bmod M$$
$$h(P) = (P_0 + \sum_{n=1}^{N-1} P_n\cdot A^n) \bmod M$$
그리고 P_0을 제외한 $$\sum_{n=1}^{N-1} P_n\cdot A^n$$ 식의 값이 고정된다고 가정하면 P_0이 1씩 증가함에 따라 h(P)는 마찬가지로 1씩 증가함을 알 수 있다. 단, mod M을 해주기 때문에 그 범위는 0부터 M-1까지일 것이다.

P_0이 나올 수 있는 경우의 수는 0부터 M-1까지이므로 M개.
그에 각 P_0에 따라 P_1부터 P_N-1까지 나올 수 있는 경우의 수는 M^{N-1}개이며,
그리고 각 h(P) 값에 해당되는 비밀번호의 경우의 수는 모두 같다.
즉, 해시값이 일치하는 비밀번호는 M^{N-1}개이며, 이를 1 000 000 007으로 나눈 나머지를 출력하면 되는 것이다.
아이디어 구체화가 오래 걸렸다.
코드는 단순할 것으로 예상된다.
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String[] strings = scanner.nextLine().split(" ");
// a와 h는 필요 없는 데이터이므로 무시.
int n, m;
n = Integer.parseInt(strings[0]);
m = Integer.parseInt(strings[1]);
scanner.nextLine();
System.out.println((int)Math.pow(m, n-1)%1_000_000_007);
}
}하지만 이렇게 하니 틀렸다고 나온다.

두 번째 입력 예제를 보니 n의 값이 5백만, m의 값이 5백만이다.
그럼 확실히 문제가 생길 수 있음을 예상할 수 있다.
int의 범위는 약 21억까지니까...
그래서 long을 사용하고, for문을 도는 것으로 바꾸었다.

그렇다면 나머지를 구하는 식을 for문과 같이 돌아줘야 하나?
이랬을 때 결과에 문제가 없는지 검증이 먼저 필요하다.
public class Main {
public static void main(String[] args) {
int a, b, c;
a = 5;
b = 3;
c = 4;
int result = 1;
for(int i=0; i<a-1; i++){
result = result * b % c;
System.out.println(i+"번째 result = " + result);
}
System.out.println((int)Math.pow(b, a-1)%c);
}
}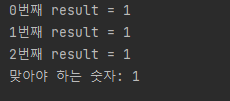
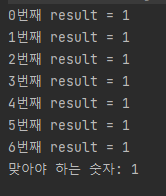

랜덤한 숫자로 검증해본 결과 문제가 없는 것을 확인할 수 있다.
그래서 바로 제출해보았다.
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String[] strings = scanner.nextLine().split(" ");
// a와 h는 필요 없는 데이터이므로 무시.
int n, m;
n = Integer.parseInt(strings[0]);
m = Integer.parseInt(strings[1]);
scanner.nextLine();
long result = 1;
for(int i=0, iMax = n-1; i<iMax; i++){
result = result * m % 1_000_000_007;
}
System.out.println(result);
}
}
테스트 케이스가 많은가? 싶어서 어제 배운대로 다시 바꿔보았다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n, m;
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
st = new StringTokenizer(br.readLine());
long result = 1;
for(int i=0, iMax = n-1; i<iMax; i++){
result = result * m % 1_000_000_007;
}
System.out.println(result);
}
}
'알고리즘 문제 풀이' 카테고리의 다른 글
| 백준1158번) 요세푸스 문제 (1) | 2023.05.14 |
|---|---|
| 프로그래머스) 의상 (0) | 2023.05.11 |
| 프로그래머스) 나누어 떨어지는 숫자 배열 (0) | 2023.05.10 |
| 백준10818번) 최소, 최대 (0) | 2023.05.10 |
| 프로그래머스) 기능개발 (0) | 2023.05.09 |




